電圧源・電流源・出力インピーダンス
新しい電池と古い電池の例
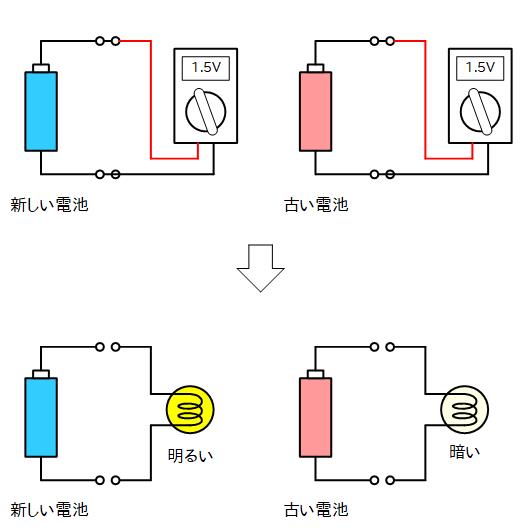
ここに新しい電池と古い電池があります。
テスターで電圧を測ると、右図のようにどちらも 1.5V を指します。
ところが豆電球を繋いでみると、新しい電池では明るく点灯しますが、古い電池では暗くしか光りません。
これは電池の特性がテスターで測定される電圧だけでは表せないということを示しています。
実は電池には内部抵抗というものがあり、等価回路で書くと下のようになります。
ここで、E0 は電池の起電力を表し、新しい電池でも古い電池でもその値は変わりません。
R は豆電球の負荷抵抗に相当し、ρは電池の内部抵抗を表します。
新しい電池では内部抵抗が小さく、古い電池になると内部抵抗は大きくなってきます。
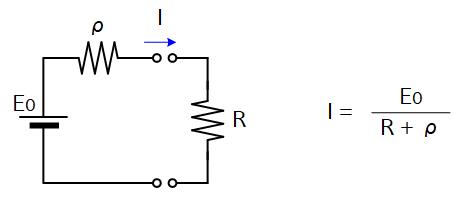
左図の流れる電流の式から明らかなようにρが大きくなると流れる電流は小さくなります。 すなわち、古い電池ではρが大きいために流れる電流が小さくなって豆電球は暗くなるということが分かります。
このように電池の特性を決めるのは起電力 E0 だけではなく、内部抵抗 ρも関与していることが分かります。
※ テスターで測定した場合に両者の電圧が等しくなるのは、テスターの負荷抵抗がほぼ無限大だからです。
電流の式から明らかなように、R=∞ の場合には電流はゼロになり、ρによる電位降下が起きないために、新しくても古くても起電力 E0 がそのまま観測されます。
電気信号を観測する場合は一般に電圧を測定しますが、その信号のインピーダンスを意識する必要があります。
電圧源と電流源
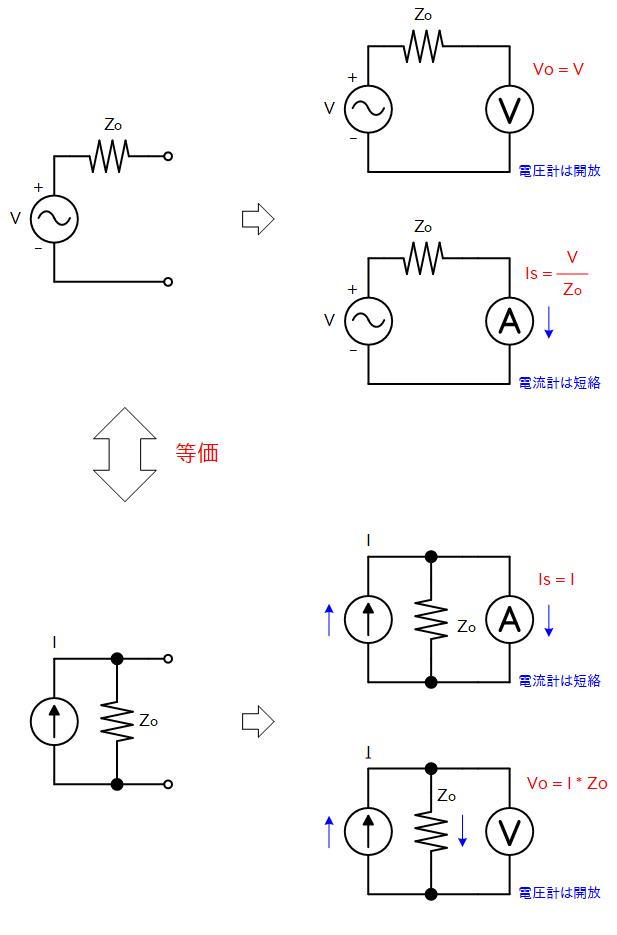
信号源は右図のように電圧源と出力抵抗で表され、開放電圧 (Vo) と、短絡電流 (Is) 、出力インピーダンス (Zo) の三つの特性で特徴づけられます。
開放電圧は端子間を開放したときに観測される電圧 (Vo) で、内部の電圧源の電圧がそのまま現れます。
短絡電流は端子間を短絡したときに観測される電流 (Is) で、電圧源の電圧、すなわち Vo を出力インピーダンス (Zo) で割った値となります。
以上から、Vo, Is, Zo の3つの特性のうち、2つの特性が決まると残る1つはオームの法則で自動的に決まることが分かります。
なお、Zo がゼロの場合は理想電圧源で、負荷電流がいくら変化しても端子間の電圧は変わりません。
信号源を電圧源と出力インピーダンスで表すことは理解しやすいですが、電流源と出力インピーダンスで表すことは馴染みが少ないかもしれません。 必要に応じて使い分けをします。
信号源をブラックボックスとして外部から見た時には、開放電圧と短絡電流と出力インピーダンスという特性でしか内部を知る由がありません。 言い換えるとそれらの特性が同じであれば内部が電圧源からできているのか電流源でできているのかは不問です。
電圧源と見るか、電流源と見るかは設計者の考え方次第です。
回路を読み解く場合に、都合のよい見方をすれば良いと思います。
キルヒホッフの法則
キルヒホッフの電流則
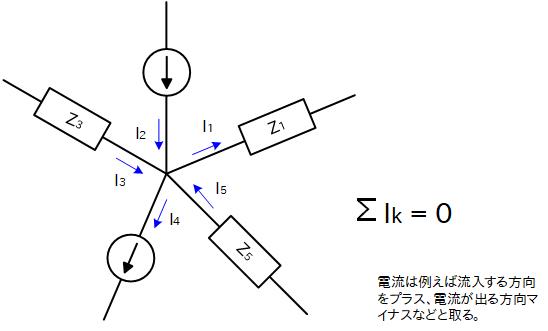
キルヒホッフの電流則は、あるノード (節点) について、出入りする電流の総和はゼロになるというものです。
例えて言うなら、川の分岐や合流のようなもので、どこからも水は湧き出ないし、消えたりもしないということを意味します。
これは当たり前といえば当たり前ですが、小信号解析などで方程式を立てるときによく使います。
なお、電圧源は短絡とみなしますので、電流はそのまま素通りし、電流の出入りはありません。
キルヒホッフの電圧則
キルヒホッフの電圧則は、あるループ (経路) について電位降下と起電力の総和がゼロになるというものです。
例えて言うなら、ジェットコースターのように最初に坂を上った (起電力) あと、降下 (電位降下) を繰り返して最終的にもとの高さ (電位)に戻ってくるようなイメージです。
私の経験では、電流則と比べると、あまり使わない法則です。
なお、電流源は開放とみなしますので、ループの構成要件にはならないことに注意して下さい。
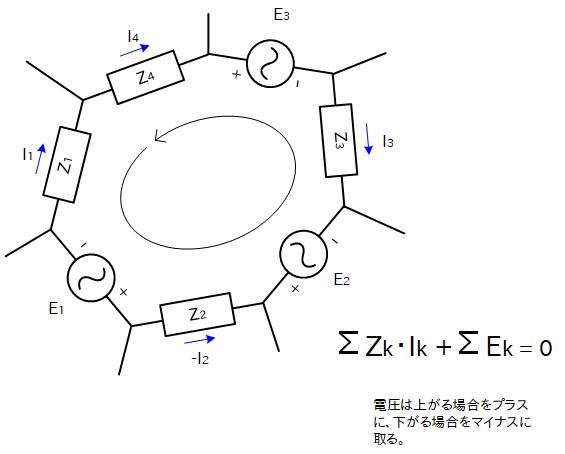
当たり前のことを言っているので軽視されがちですが、基本です…
重ね合わせの理
定理の説明
重ね合わせの理は、複数の信号源があった場合の各ノードの電圧や各パスの電流は、各信号源による電圧・電流をそれぞれ個別に求めて、それらを重ね合せたものに等しくなるというものです。
これは単純に電気回路では「線形性」が担保されていると言い換えることができます。
信号源が複数ある場合には回路が複雑になり、あるノードの電圧やあるパスの電流を求めるのが面倒な場合がありますが、重ね合わせの理を用いると非常に簡単に求めることができます。
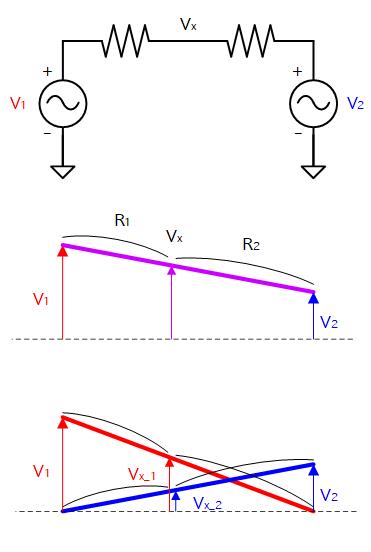
例えば右図では2つの電圧源 (V1, V2) の間を抵抗分圧した中点
(Vx) の電圧を求める例を示していますが、Vx は V2 を無視して V1 だけがある場合に現れる電圧 (Vx_1) と、V1 を無視して V2 だけがある場合に現れる電圧 (Vx_2) の和になります。
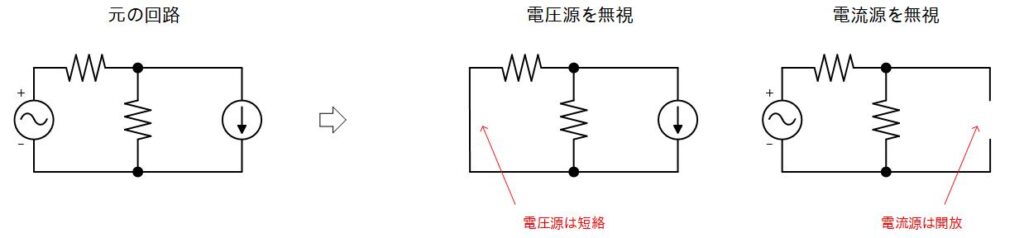
電圧源と電流源が混在する場合
信号源として電圧源だけではなく電流源も混在する場合があります。
前節で示したように電流源を電圧源に置き換えるという手もありますが、ちょっと厄介かもしれません。
その場合は、電流源は短絡、電流源は開放として重ね合わせの理を使うことができます。
必ずしも必要とは限りませんが、これを使うと計算が単純化できる場合があります。
テブナンの定理
定理の説明
回路内の任意の2っ節点間に接続された負荷インピーダンス (Zl) を流れる電流 Io は、負荷 (Zl) を切り離したときに現れる電位差 Vo と、この2接点間より回路を見たインピーダンス Zo を用いて下式のように書けるというのがテブナンの定理です。
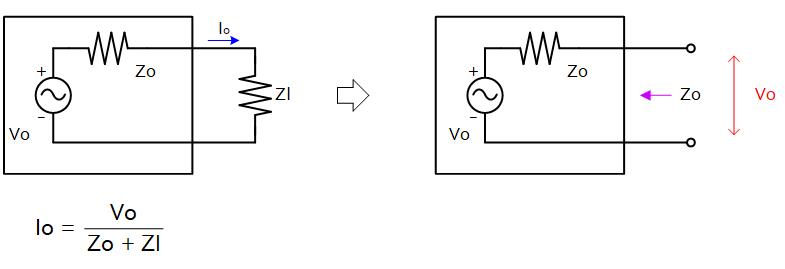
これは内部の回路がどう作られているかは不問 (ブラックボックス) でも、外部からどう見えるか (開放電圧とインピーダンス) ということで
電圧源と抵抗からなる等価回路に変換できるということを意味しています。
応用例
左図の回路に 10Ωの負荷を接続したときに負荷に流れる電流を求めることを考えます。
キルヒホッフの法則を使って地道に解くことも可能ですが、結構めんどうな計算が必要です…
なので、テブナンの定理を利用するためにまずは破線の箇所で切り離して、左側だけを取り出してみます。
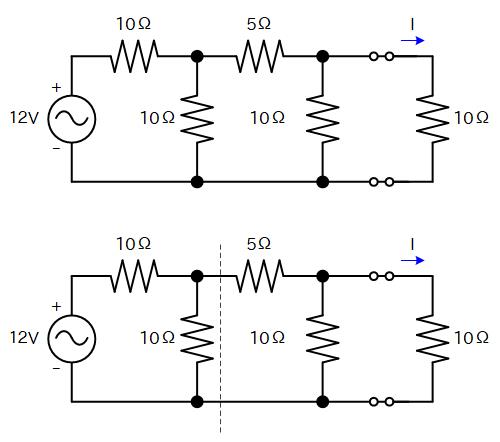
最初に開放電圧を調べますが、これは 12V を 10Ωづつの抵抗で分圧するので、現れる電圧は Vo = 6V になります。
次にインピーダンスを調べます。
インピーダンスを見る場合は電圧源は短絡と考えます。
端子の切り口から見ると、 10Ωの抵抗が並列に接続されていますので、インピーダンスは 5Ωです。
したがって、開放電圧とインピーダンスの関係から矢印のような一つの電圧源と一つの出力抵抗という等価回路に置き換えることができます。
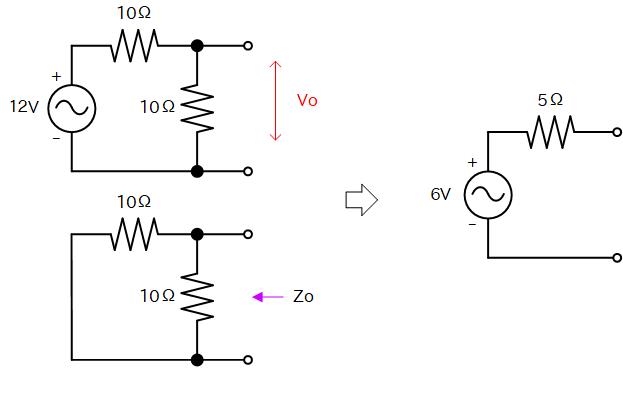
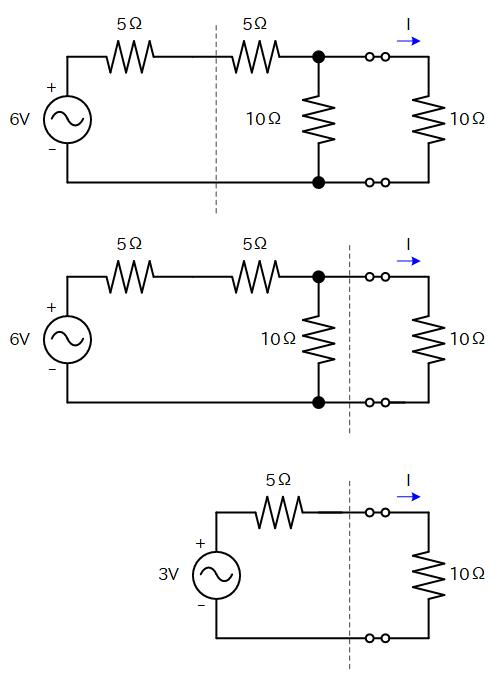
この等価回路を元の回路に戻すと、回路がだいぶ簡略化されていることが分かります。
これを繰り返すことで、最終的にもとの回路が電圧源と抵抗というシンブルな等価回路になり、負荷に流れる電流を簡単に求めることができます。
これがテブナンの定理のよくある応用例です。
ただ、現実問題として、例に挙げたような回路を目の当たりにすることはまずありません…
ただ、どんな信号源も電圧源と出力抵抗で現されることは理解しておいた方が良いでしょう。
※ テブナンの定理を使うと理解しやすい回路の例として、 R-2R の
D/A コンバータがあります。
これについてはまた別の機会に解説したいと思います。
頻繁に使う法則ではありませんが、回路の単純化したい場合などに役に立ちます。
小信号解析と4端子回路網
小信号解析の意味
アナログではよく “小信号解析” という手法を使います。 この “小信号” というのがアナログ回路を勉強する際に結構わかりにくい考え方の一つです。
アナログ回路は、一般的にある DC 動作点を与えて、その動作点を中心に AC 信号を重畳するという使い方をします。
具体的に右図のような回路を考えてみます。 ここでは CMOS インバータの入力と出力が抵抗で接続されています。 CMOS インバータなので、入力電流は流れないため、抵抗による電位降下は発生せず、Vin と Vout は同電位になりますので赤のグラフのように Vout = Vin という関係が成り立ちます。 一方、CMOS インバータの入出力特性は青のグラフのように表されます。 この2つのグラフの交点が動作点 (Vop) となり、Vsig が変化すると Vout はこの Vop を中心として変化することになります。
このとき Vop のポイントでの CMOS インバータの入出力の傾きを G= (dVout/dVin) とすると、Vsigの微小変化ΔVsig に対して、出力はΔVout=G×Vsig の変化が得られます。 すなわち信号が増幅されるということになります。
このように、信号振幅が小さい場合の応答を調べることを小信号解析と呼びます。
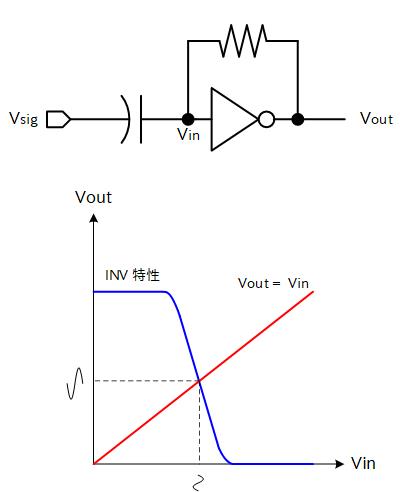
CMOS インバータの特性は非線形性ですが、振幅が小さい場合は線形近似が可能です。
一般的に非線形素子で回路が構成されている場合はシミュレーションなどでしか振る舞いを求めることはできませんが、線形素子の場合には解析的に、すなわち手計算で入出力特性などを求めることができます。 これが小信号解析を行う理由です。
さらに言えば、非線形素子を電圧源や電流源および抵抗やコンデンサなどの線形素子で記述して、小信号解析を行うのが一般的(古典的)なアナログの手法と言えます。 古典的ではありますが、回路の本質的な動作限界を見極めたり、シミュレーション結果の妥当性を確認できるなど、現代でも非常に有用な設計手法です。
4端子回路網
前節で小信号解析に触れましたが、小信号解析と相性がよく、古典的なアナログ設計では良く使われるものに、4端子回路網という概念があります。
これは回路を入力と出力からなるブラックボックスと考え、入力の電圧・電流に対する出力の電圧・電流の関係を4つのパラメータで記述するという解析手法です。 中身が違っていても、入出力の振る舞いが同じであれば、外から見る限り同じ回路として扱って良いということを意味しています。
代表的な4端子回路パラメータとしては g パラメータとz パラメータがあり、定義は右図の通りです。
ここで、各パラメータが偏微分で示されていることに注意して下さい。微分ということは微小な入力変化に対する微小な出力変化の割合で定義ということになり、まさしく小信号解析の考え方そのものです。
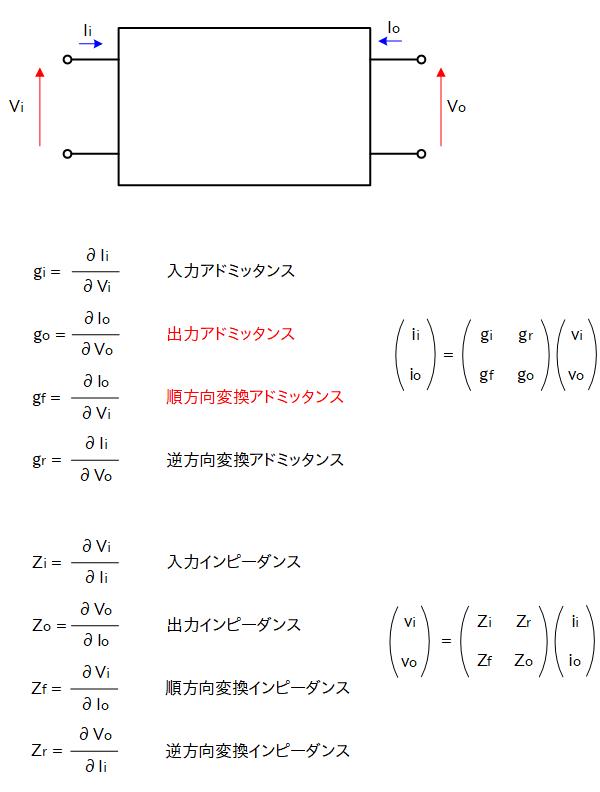
MOS トランジスターを等価回路で表す上で非常に重要なパラメータが gパラメータの順方向変換アドミッタンスと出力アドミッタンスで、MOSトランジスタの場合には それぞれ gm (相互コンダクタンス)、gds (ドレイン-ソース コンダクタンス) と呼ばれます。
ただ gds については、逆数をとって rds (ドレイン-ソース抵抗) で表すことがあります。
というより、私の場合は gm と rds という組み合わせを良く使います。
(当然 gm と gds で記述している書籍や論文もありますが、好みの問題になるかと思います…)

小信号解析はよく使う設計手法ですが、4端子回路網という概念は正直それほど使いません。 トランジスタなどの非線形素子をモデル化する時にちらっと出てくる程度かと思います。




コメント